Discrete cosine transform

BlaBla
1

Hello,

Poursuivant ma quête pathétique de ne pas mourir complètement con, j’ai décidé d’essayer de comprendre les FFT, pas à pas. Etant donné que la Cafzone pullule de gens qui se la touchent en DSP, je me dis que je pourrais sûrement trouver un peu d’aide ici, afin de me préparer au tournage de l’émission “confessions intimes” sur le sujet “je ne comprends rien aux transformées de Fourier, et cela ruine ma vie sociale”.

Pour commencer, j’ai décidé de me fixer un objectif simple : je crée un petit set de données à une dimension, sous forme d’une somme de cosinus avec des phases, des amplitudes, et des fréquences différentes, je sample et je quantize (vivent les anglicismes), et maintenant je veux retrouver mes coefficients d’origine à partir du résultat. C’est bon, c’est bien à ça que sert une DCT ? Voici mon set de données, en image.

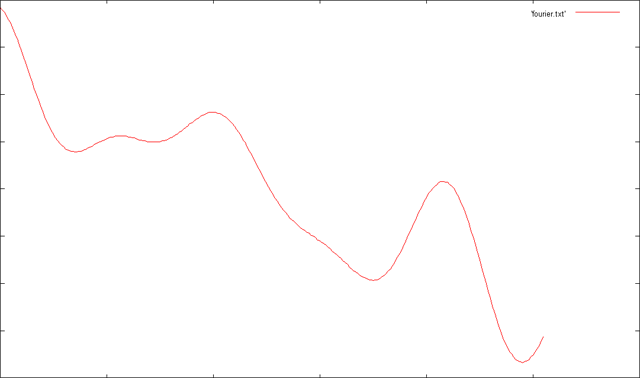
Maintenant j’ai trouvé plein de formules de DCT, en fonction des effets de symétrie attendus dans les data, et dont on me dit que la DCT II est la plus courante. Ok, donc cette formule est basée sur des paramètres, le but du jeu est de trouver les paramètres qui feront que la fonction s’approchera le plus des données. Donc là il faut appliquer un algorithme, et y’en a une chiée, surtout dans la catégorie FFT. Mes connaissances en math étant anecdotiques une fois sorti de ce qui touche à la 3D, ça n’aide pas vraiment. Mais ce que j’aimerais dans un premier temps, c’est comprendre quelle est la façon la plus élémentaire de déterminer ces paramètres. Sans notion de performance, juste quel raisonnement on peut appliquer à ce genre de choses.

2

TableCurve est ton amie :slight_smile: On se sert de ca au taff pour generer les equations de progression non lineaires, en fonction des données qu’on veut.

3

C’est exactement ce que j’ai fait en cours …
j’essayerai de mettre à jour quand j’aurai relu (et accessoirement un peu compris) mes tds.
Sinon t’as d’autres trucs pour faire de l’approximation plutôt que fourrier, pour info.
en vrac t’as les polynomes de lagrange, ou de taylor, les formules sont peut-être plus simple “juste pour approcher ta courbe pour voir”

4

Merci pour ces réponses, mais en fait ce qui m’intéresse au final, c’est comprendre plus en détails les méthodes de compression lossy basées sur les DCT, et si possible par la pratique. Y’a-t-il des systèmes de compression basés sur d’autres types de curve-fitting qui s’avèrent plus simples à appréhender ? Il me semble que les wavelets sont vagument (haha) basées sur la même idée, mais que c’est encore bien plus compliqué.

C’est probablement idiot comme question, mais les NURBS n’ont aucune application niveau compression ?

5

tout depends ce que tu veux compresser… Si tu as un liste de points que tu veux compreser tu fit un Spline et hop tu as compressé ta donnée.

A la question originelle sur les DCT c est plus du tout frais dans ma mémoire alors je me taie pour ne pas dire une connerie.

Et pour les wavelets / curvelets oui c est bassé sur des transformées en frequence.

Si tu es vraiment interessé par ce sujet Mr. Meyer est ton homme : http://en.wikipedia.org/wiki/Yves_Meyer je l ai eu en court c est un delice.

Bon courage.

6

Bon, je ne connais pas ton niveau en Maths, mais je vais supposer que tu as des connaissances d’algèbre linéaire. Je vais simplement expliquer la transformée de Fourier (pas le FFT ou la DCT que je n’ai jamais utilisées).

En gros, on sait que toute fonction périodique de période 2pi peut être décomposée en une somme (potentiellement infinie) de sinus et de cosinus (de période 2pi/k avec k entier) et que ces sinus et cosinus sont orthonormaux.

Je rappelle qu’une base est orthonormale si pour tous vecteurs x et y de la base, on a x.x = y.y = 1 et x.y = 0, où . désigne le produit scalaire. Ah mais c’est quoi le produit scalaire entre deux fonctions ?

On définit le produit scalaire canonique entre deux fonctions périodiques f et g de période 2pi par l’intégrale de 0 à 2pi de fg* avec g* la fonction conjuguée de g.

Le but du jeu est donc, étant donnée une fonction f, de retrouver ses coefficients dans la base de sinus et de cosinus. Mais, lorsque la base est orthonormale, c’est très facile de faire ça ! Il suffit de calculer le produit scalaire de la fonction f avec chaque vecteur de base. Le résultat est le coefficient voulu.

Une transformée de Fourier va donc calculer les intégrales de fsin ou fcos entre 0 et 2pi pour trouver les coefficients. Une fois que tu les as, tu ne vas garder que les plus élevés et mettre tous les autres à 0.

La transformée de Fourier discrète ne va pas calculer l’intégrale du produit sur tout le signal (puisque tu n’as qu’un signal samplé) mais va faire la somme correspondante sur tous les points où tu as un échantillon.

Je sais pas trop si c’est clair, mais ça te donnera peut-être les bases pour comprendre l’article de Wikipédia.

Edit: Koubiak, j’ai eu Meyer en cours aussi (Mallat en donnait, mais je n’y ai pas assisté…). Tu as fait le DEA MVA de Cachan ou autre chose ?

7

Le gros avantages des transformées en fréquence est qu’elles te permettent de représenter tes données dans un espace ou il est plus facile d’appliquer des traitements psycho-acoustiques (ou psycho-visuels pour la compression d’images) pour supprimer les informations les moins perceptibles.

Tout les algos n’utilisent pas forcément la DCT (même si c’est la plus utilisée car relativement rapide). AC3 utilise par exemple une FFT modifiée.

Par contre tu as des algos qui vont utiliser des aproximations matématiques toutes autres, mais cela donne en général de bien meilleurs résultats avec des taux de compressions faibles. Cela permet, en stockant la différence entre l’approximation et la source, d’avoir des taux de compressions en lossless très sympatiques …
Jette un oeil sur les specs DTS, si tu peux, c’est une approche de ce type.

8

Oui j ai fait MVA. Et j ai eu meyer. Mallat n’avait pas encore repris le flambeau. Je viens dailleurs de matter le nouveau programme. Il est meilleurs que quand j y etait… surtout plus touffu dans ce qui pourrait m interresser maintenant.

J y etais en 2004/2005 et toi?

Pardon pour le HS les gens

9

Ouhhhhhhh j’ai rien compris.

10

SuperLegume, c’est loin mais si je raconte pas de conneries (et je manque surement de rigueur mais bon en gros…) c’est tout simple, t’as une base orthonormale (comme en 3d XYZ), et tu decompose une vecteur sur les composants des cette base (en 3d, X/Y/Z) et ca te donne des cooefs (X=3,Y=4,Z=-5 ou n’importe). En 3d la maniere dont ca se trouve c’est de faire V.(1,0,0) pour X par exemple avec “.” qui est le produit scalaire dans ton espace vectoriel.

Une fonction peut etre un “vecteur” et une base etre composee de tout un tas de fonctions. Selon ce que tu veux faire tu choisit ta base (le jeu de fonction) pour t’aider, par exemple avec Fourier, la base, c’est les fonction trigo de base et ca te donne une idee de comment ton signal se decompose en somme de ces fonctions (de la meme maniere qu’un vecteur dans l’espace c’est la somme du vecteur sur X, Y et Z). Un des inconvenient de Fourier, c’est que c’est la merde avec l’information temporelle (les cos/sin c’est des fonctions grave periodiques) donc des fois selon ce qu’on veut faire, on decompose sur une base differente. Pour compresser c’est sympa parceque par exemple apres avoir decompose, si au dessus d’un certain point t’entend plus les frequences par exemple, tu les degage une fois decomposees facilement, tu refais ta somme et t’as un signal qui sonne pareil mais qui contient moins d’information (donc qui se compresse mieux).

11

Je… suis… un… littéraire… cerveau… saturé… autodestruction.

12

Sauf que les maths c’est beau. Et la beauté c’est universel :slight_smile:

13

Vite fait, parce que j’ai l’impression que tout un tas de trucs se melangent dans le discours (mais c’est ptet moi qui capte rien):

Transformée de Fourier: transformation d’un signal (en fonction du temps continu) en sa représentation en fonction de la fréquence (ce que genji a raconté, de facon succinte)
DFT (discrete fourier transform): transformée de Fourier sur un signal non-périodique (ce qui est le cas de tes signaux, puisqu’ils sont finis) et temps discret (ce qui est le cas, puisque tes signaux sont samplés)
(d’ailleurs, tout signal qui est enregistré dans un ordinateur est fini et discrete-time, par définition)
FFT (fast fourier transform): catégorie d’implementation des DFT (qui a l’avantage d’etre rapide, par rapport au calcul basique de l’intégrale)
O(N^2) pour l’integrale, O(N logN) pour les FFT
DCT (discrete cosine transform): autre transformée (a laquelle je n’ai pas touché depuis bien longtemps) pour passer du time-domaine au frequency-domain. Je ne veux pas rentrer dans les details de la DCT parce que ce n’est pas frais, mais il semble important de bien maitriser les 3 premiers points avant de passer a la DCT.

Mais bon, le mieux ce serait que tu te fasse expliquer tout ca par le maitre:
http://ccrma.stanford.edu/~jos/mdft/mdft.html

Julius O Smith est un excellent pedagogue et ses livres on-line sur le DSP sont ma reference. En plus, dans ce livre, apres avoir introduit la DFT, il fait un recapitulatif plutot couillu des nombres complexes et de la theorie du signal.

14

Merci à tous pour vos réponses !

genji : effectivement expliqué comme ça, y’a déjà une série de points qui sortent de l’obscurité, je vois un peu mieux dans quoi je m’avance.

Tzim : yep, sur le principe et les applications je comprends (enfin je pense).

GloP : j’en étais arrivé à la même représentation conceptuelle, maintenant j’ai confirmation de ne pas trop divaguer.

LodeRunner : à première vue, ce livre est LA référence qu’il me faut pour bien tout comprendre, merci !

15

J’adore la Zone pour ca.

aujourd’hui, j’y ai entre autre, matte des petites culottes :cry: , reflechis sur l’avenir du jeux video sur pc :crying: , echange (surtout recus) des infos sur GTA4 :stuck_out_tongue: et revu des vielle notions de math/physique oubliee depuis l’unif :slight_smile: .

j’adore :smiley:

16

Heureusement que t’étais là, je commence à lire le premier pavé, je vois 2 anagrammes inconnus, hop défilement rapide jusqu’à tombé sur DTC. Là je me dis « oh un truc con à lire ». Même pas, c’était juste un DCT. Bref la loose ^^

17

[quote=« Boltac, post:15, topic: 47458 »]J’adore la Zone pour ca.

aujourd’hui, j’y ai entre autre, matte des petites culottes :stuck_out_tongue: , reflechis sur l’avenir du jeux video sur pc :cry: , echange (surtout recus) des infos sur GTA4 :smiley: et revu des vielle notions de math/physique oubliee depuis l’unif :slight_smile: .

j’adore :D[/quote]

+1
Je vous aime les gars ! :crying: